Euler: The King of Mathematics

Euler, Lagrange, James Webb Telescope, and Aditya-L1

Back in school, everyone must have tried solving that puzzle where you had to draw the figure shown without lifting your pen.
A puzzle that never seemed solvable!
However, I had no idea then that this puzzle—known as the Konigsberg Bridge Problem—was so famous in history.
The great mathematician who solved this puzzle and expressed it in a formula was none other than the legendary Leonhard Euler.
Euler’s mathematical work was vast—so vast that it directly connects to modern marvels like the James Webb Space Telescope and India’s Aditya-L1 mission.

India recently launched the Aditya-L1 spacecraft to study the Sun.
It is now stationed at a point called L1, located between the Sun and Earth.
Earlier, NASA had placed the James Webb Space Telescope (JWST) near the L2 point.
The unique property of these points is that the total gravitational force from surrounding bodies balances out to zero here.
Just like if two people of equal strength pull an object from opposite sides, it will not move—similarly, the Sun, Earth, and Moon’s forces balance at these points.
At such locations, spacecraft or telescopes can remain stationary relative to Earth without burning fuel.

There are a total of five such points, called Lagrangian Points—L1, L2, L3, L4, and L5—shown in the diagram.
Although all five are named after mathematician Joseph-Louis Lagrange, only L4 and L5 were calculated by him.
L1, L2, and L3 were actually discovered earlier by Euler through mathematics (in his works E327 and E400).
In 1767, he proved their existence using a quintic equation (fifth-degree equation), and these three points were collinear.
Later, in 1772, Lagrange published his research adding the other two points—L4 and L5.
Lagrange’s contributions to mathematics were equally monumental—he refined Newton’s mathematics and made it more accessible, often collaborating with Euler.

Euler was born on 15 April 1707 in Basel, Switzerland, to Paul Euler, a government official, and Margaret.
He was their first child, followed by two sisters, Anna and Maria.
After completing primary education, at just 13 years old (in 1720), Euler entered the University of Basel.
There he met the famous mathematician Johann Bernoulli, a professor of mathematics and philosophy.
During his first two years, Euler studied geometry and both theoretical and practical arithmetic.
Fluent in Latin, he graduated in 1723 with a Magister Artium degree, delivering a Latin lecture on Descartes and Newton.
Much of his life was later spent in Russia and Germany.

In 1727, Euler took part in a unique mathematics competition titled Thoughts about a nautical problem on the positioning of masts.
The task was to determine the optimal sail size for maximum speed, considering wind, boat shape, and other factors—something Euler had never seen in real life, as he had never encountered large ships before the age of 20!
For many years, the competition was won by Pierre Bouguer, a renowned French mathematician and sailor.
That year, Bouguer won again, but the young Euler astonished everyone by solving the complex problem and securing second place.

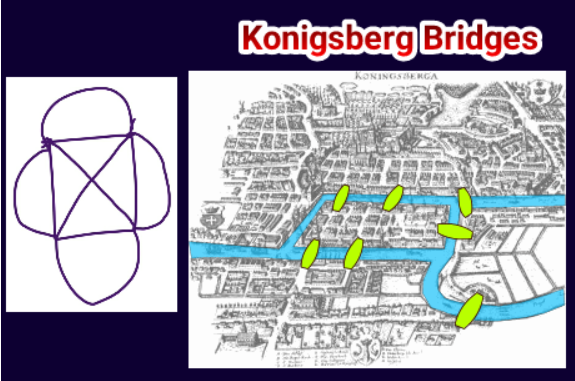
In 1736, Euler solved the aforementioned Konigsberg Bridge Problem.
The city of Königsberg (in present-day Russia) was divided by the Pregel River and had an island connected by seven bridges.
The challenge was to determine whether it was possible to cross each bridge exactly once.
Euler not only solved it easily but also created a formula for it, laying the foundation of graph theory.

The years 1750–1756 marked the golden era of Euler’s life.
He worked on numerous topics, including calculations for the equinoxes and three-dimensional geometry, in which he presented the famous formula S + H = A + 2 (where S = vertices, H = faces, A = edges).

Euler’s contributions were enormous—he worked in almost every branch of mathematics: geometry, calculus, cartography, trigonometry, algebra, number theory, as well as in physics, lunar theory, and other sciences.
Surprisingly, he also studied music theory, applying mathematical principles to it.

Euler was familiar with Indian calendars, lunar months, and astronomy.
Orientalist Gottlieb Bayer, who studied Asian—especially Indian—mathematics and astronomy, sent Euler his book Historia, along with additional notes from his friend Walther.
He posed some unsolved questions and asked Euler to provide a detailed analysis.
Euler replied with 21 analytical points, offering several formulas that greatly aided Bayer’s research—though Euler himself had limited interest in that particular area.

If all of Euler’s work, including fundamental theorems, were published, it would fill 45,000–50,000 pages!
He wrote over 4,500 letters and hundreds of manuscripts.
It is estimated that one-fourth of all research in 18th-century mathematics, physics, engineering, mechanics, astronomy, and navigation was Euler’s alone.

Despite losing his eyesight later in life, Euler’s passion and command over mathematics never waned.
Remarkably, half of his work was produced after he became completely blind!

On 18 September 1783, at the age of 77, the life—and mathematics—of this extraordinary genius came to a close.

References:

• Euler’s published research (Papers on the Three-Body Problem)

• Leonhard Euler: Mathematical Genius in the Enlightenment – Ronald Calinger